Difference between revisions of "Formulae"
| Line 18: | Line 18: | ||
</math> | </math> | ||
| + | Now we sum all of the factors for all augmenters together. | ||
| + | |||
| + | <math> | ||
| + | F_sum = F_1 + F_2 + F_3 + F_4 + F_5 + F_6 + \cdots | ||
| + | <math> | ||
===Augmenter Tweaking=== | ===Augmenter Tweaking=== | ||
Revision as of 20:18, 16 September 2010
This is an explanation page for the various formulae involved in calculating stats in game.
Contents
[hide]Augmenter Addition
Augmenter addition is a multi-step process. First all augmenters are tweaked using the augmenter tweaking formula below.
Then the tweaked bonus is converted to a factor (F) using one of two formula, depending on if it is a positive augmenter or a negative augmenter. If the tweaked augmenter gives +83% then by adding 1 the tweaked bonus (B) is 1.83. In a similar fashion, if the tweaked augmenter gives -83% then B is .17.
For positive augmenters:
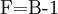
For negative augmenters:
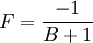
Now we sum all of the factors for all augmenters together.
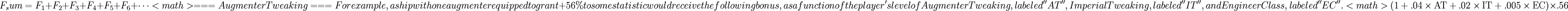
Similarly, if the equipped augmenter granted -56% instead, the resulting penalty is calculated as follows.

Speed
Speed is defined as distance traveled per second.
Thrust
Acceleration (a) is Thust (T) divided by Weight (W). Acceleration is defined as Speed per second.

Turning
Turning (T) in revolutions per second is equal to the turning listed on an engine (t) times 152 divided by Weight (W).
